1. 优化算法

1.1 SGD的问题

  • 一些方向变化太快，一些方向变化太慢，就会要么很慢要么抖动很厉害
  • 出现局部极小值或者马鞍点
    • 这些位置梯度为0，在高维度的情况下，马鞍的情况更加常见
    • mini batch会产生大量的noise，下降更加糟糕

1.2 SGD + Momentum

就是要参考前一次的下降方向。 前一次的下降方向就叫做Momentum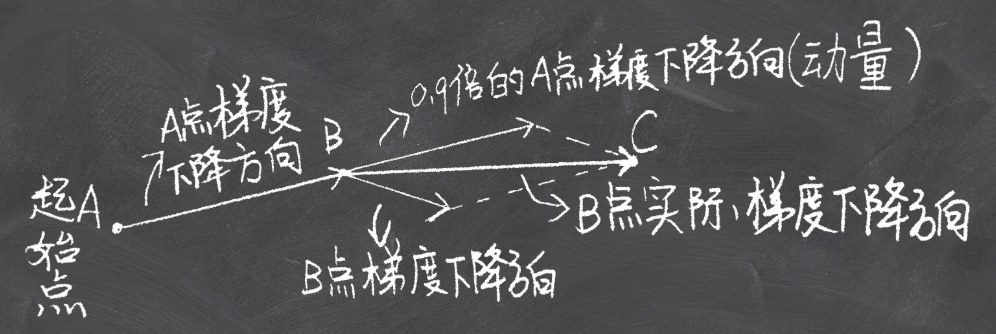： image.png 算法：

# Computing weighted average. rho best is in range [0.9 - 0.99]
V[t+1] = rho * v[t] + dx
x[t+1] = x[t] - learningRate * V[t+1]

1.3 Nestrov momentum

就是新增了超前点的概念。也就是上次下降方向的预计到达的点就是超前点，是计算超前点的梯度，将那个超前点处的梯度和超前向量相加得到实际的方向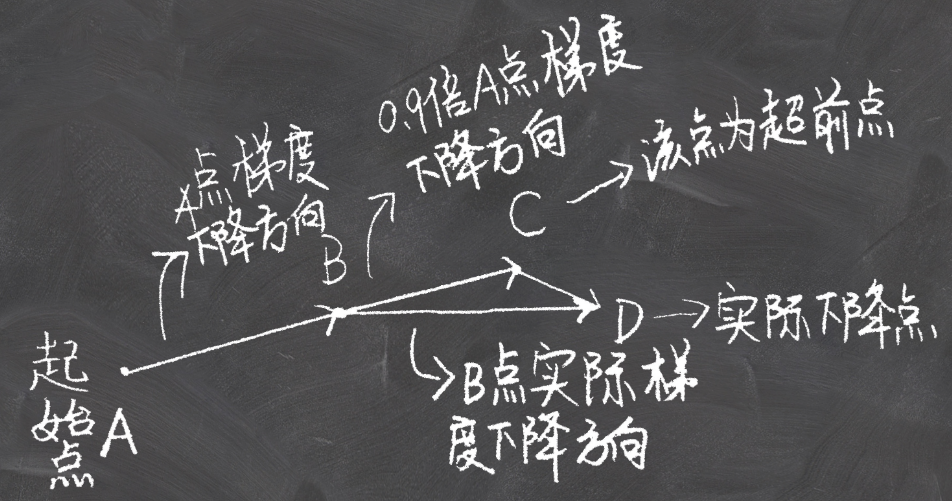： image.png 大致的公式推导： image.png

1.4 AdaGrad

由于之前的lr(learning rate)是固定不变的，adagrad就是动态的改变lr。

但是该方法有点僵硬，就是让lr一直减小的，有可能导致还没有到最小点就梯度为0不动了（因为里面的grad_squared一直的增大）：

grad_squared = 0
while(True):
  dx = compute_gradient(x)
  
  # here is a problem, the grad_squared isn't decayed (gets so large)
  grad_squared += dx * dx			
  
  x -= (learning_rate*dx) / (np.sqrt(grad_squared) + 1e-7)

1.5 RMSProp

就是对adagrad的改进，使得其只是利用最近一段时间的梯度作为除数：

grad_squared = 0
while(True):
  dx = compute_gradient(x)
  
  #Solved ADAgra
  grad_squared = decay_rate * grad_squared + (1-grad_squared) * dx * dx  
  
  x -= (learning_rate*dx) / (np.sqrt(grad_squared) + 1e-7)

这里(decay_rate * grad_squared + (1-grad_squared) * dx * dx)其实是对二阶动量进行了指数移动平均：

https://zhuanlan.zhihu.com/p/38276041

1.6 Adam

就是RMSprop和Momentum的结合。 不仅对二阶动量进行了指数移动平均，而且对一阶动量也进行了指数移动平均

1.7 二阶优化

L-BFGS

In practice first use ADAM and if it didn’t work try L-BFGS！

2 正则化

2.1 model ensembles

  1. Train multiple independent models
  2. At test time average their results

一般会有2%的效果提升

2.2 dropout

前向传播的时候，随机地把一些neurons设置为0

0.5的drop比率是通常的选择